
안녕하세요?
오늘은 전기수학에서 중요한 개념인 방정식에 대해 알아보려고 해요. 방정식은 전기회로에서 매우 중요한 개념이에요. 함께 공부해보면서 전기수학을 더 재밌게 공부해보세요!
| 목 차 |
| 1. 전기에서의 방정식 사용 |
| 2. 1차 방정식 |
| 3. 2차 방정식 |
1. 전기에서의 방정식 사용
방정식은 미지수와 그에 따른 관계를 수학적으로 표현하는 수학적 도구입니다.
방정식을 사용하여 전기회로의 전류, 전압, 저항 등을 구하고, 전력 시스템에서의 전력 손실 등을 예측할 수 있습니다. 전기수학에서는 주로 1차방정식과 2차방정식을 다루며, 이들을 풀이하는 과정은 전기공학 학습에 있어서 필수적인 내용입니다.
2. 1차 방정식
①1차방정식 정의
1차방정식은 다음과 같은 형태를 갖습니다
ax + b = 0.
여기서, a와 b는 상수이며, x는 미지수입니다.
② 1차방정식 풀이 과정
- 식에서 미지수 x로만 이루어진 항을 왼쪽으로 이항시킵니다.
- 상수항을 오른쪽으로 이항시킵니다.
- 계수 a로 x를 나누어서 x의 계수를 1로 만듭니다.
- x의 계수가 1이 되었으므로, 상수항을 계수 앞으로 이항시킵니다.
- 이렇게 구한 x의 값은 1차방정식의 해가 됩니다.
③ 1차방정식 예제
2x + 3 = 7.
- 우선, x로만 이루어진 항을 왼쪽으로 이항시키면 2x = 4가 됩니다.
- 그리고, x의 계수를 1로 만들기 위해 2로 x를 나누면 x = 2가 됩니다.
- 따라서, 이 1차방정식의 해는 x = 2입니다.
3. 2차 방정식
① 2차방정식 정의
2차방정식은 다음과 같은 형태를 갖습니다.
ax² + bx + c = 0.
여기서, a, b, c는 상수이며, x는 미지수입니다.
② 2차방정식 풀이 과정
- 식에서 x의 계수를 이용해 이차항을 완전제곱 형태로 만듭니다.
- 다음으로, 이차항의 계수와 상수항을 이용하여 근의 공식을 사용하여 x의 값을 구합니다.
③ 2차방정식 예제
x ²- 5x + 6 = 0.
- 이차항이 완전제곱 형태가 아니므로, 이차항의 계수와 상수항을 이용하여 근의 공식을 사용합니다.
- 근의 공식을 적용하면 x = 2 또는 x = 3이 됩니다.
- 따라서, 이 2차방정식의 해는 x = 2 또는 x = 3입니다.
* 근의 공식
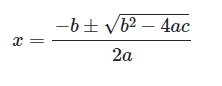
이상으로, 전기수학 방정식의 중요성에 대해 알아보고, 1차방정식과 2차방정식에 대한 용어와 풀이 과정에 대해 설명하였습니다. 전기공학 학습에 있어서 방정식은 필수적인 개념이므로, 꼼꼼하게 이해하고 연습하는 것이 중요합니다.
'전기 > 전기산업기사' 카테고리의 다른 글
| 전기수학 인수분해 이해하기 (1) | 2023.12.04 |
|---|---|
| 다항식 (0) | 2023.11.13 |
| 로그함수 (1) | 2023.10.31 |
| 지수함수 (0) | 2023.09.19 |
| 복소수의 연산 덧셈, 뺄셈, 곱셈, 나눗셈 기본 개념과 계산기 활용법 (0) | 2023.06.22 |